1.表中是道琼斯工业指数(DJIA)和标准普尔500种股票指数(S&P500)1988年至1997年对应股票的收益率资料:
年份 |
DJIA收益率(%) |
S&P500收益率(%) |
年份 |
DJIA收益率(%) |
S&P500收益率(%) |
1988 |
16.0 |
16.6 |
1993 |
16.8 |
10.0 |
1989 |
31.7 |
31.5 |
1994 |
4.9 |
1.3 |
1990 |
-0.4 |
-3.2 |
1995 |
36.4 |
37.6 |
1991 |
23.9 |
30.0 |
1996 |
28.6 |
23.0 |
1992 |
7.4 |
7.6 |
1997 |
24.9 |
33.4 |
polyfit解决
计算两种指数收益率的相关系数,分析其相关程度,以0.05的显著性水平检验相关系数的显著性。
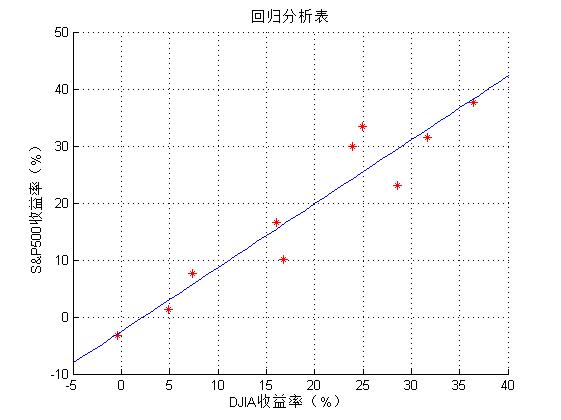
x = [16.0 31.7 -0.4 23.9 7.4 16.8 4.9 36.4 28.6 24.9];
y = [16.6 31.5 -3.2 30.0 7.6 10.1 1.3 37.6 23.0 33.4];
scatter(x,y,'r*');
xlabel('DJIA收益率(%)');
ylabel('S&P500收益率(%)');
p = polyfit(x,y,1);%1表示一次函数
hold on;
xx = -5:1:40;
yy = polyval(p,xx);
plot(xx,yy,'b-');%画出来的是光滑的曲线
grid;
title('回归分析表')
hold off;
[r,p,rlo,rup] = corrcorf(x,y)%相关分析
>> [r,p,rlo,rup] = corrcoef(x,y)
r =
1.0000 0.9481
0.9481 1.0000
p =
1.0000 0.0000
0.0000 1.0000
rlo =
1.0000 0.7903
0.7903 1.0000
rup =
1.0000 0.9880
0.9880 1.0000
>> [i,j] = find(p<0.05);
>> [i,j] = find(p<0.05)
i =
2
1
j =
1
2
%r(i,j)表示相关系数
%P表示假设检验的P-value值,P-value值越小表示的相关性越显著。
%一般以P < 0.05 为显著, P<0.01 为非常显著
附录:r(1,2) = r(2,1) = 0.9481便是相关系数,t = r*sqrt(n-2)/sqrt(1-r^2) = 8.4335,tα/2 = 2.31,则结果是显著的。
rlo和rup是r在%95可信度下的置信区间。
2.regress解决上题
x = [16.0 31.7 -0.4 23.9 7.4 16.8 4.9 36.4 28.6 24.9];
y = [16.6 31.5 -3.2 30.0 7.6 10.1 1.3 37.6 23.0 33.4];
scatter(x,y,'r*');
xlabel('DJIA收益率(%)');
ylabel('S&P500收益率(%)');
Y = y';
X = [ones(length(y),1),x'];
[b,bint,r,rint,stats]=regress(Y,X)
%下面是返回值
b =
-2.5086
1.1198
bint =
-9.3225 4.3052
0.8137 1.4259
r =
1.1918
-1.4891
-0.2435
5.7454
1.8221
-6.2040
-1.6784
-0.6522
-6.5177
8.0256
rint =
-10.0742 12.4578
-11.9810 9.0029
-9.6540 9.1671
-4.3221 15.8128
-8.7610 12.4052
-16.1645 3.7565
-11.9494 8.5926
-10.4663 9.1620
-15.8388 2.8034
-0.7121 16.7633
stats =
0.8990 71.1816 0.0000 23.5811
%ployval函数中第一个多项式系数(行向量)是按高到低,而regress中的b是从低到高,而且是个列向量,不可直
%接bb = b',若是这样还需逆置(fliplr(bb)),或者直接顺时针旋转90
%B=rot90(A):矩阵B是矩阵A沿逆时针方向旋转90。得到的
%B=rot90(A,k):矩阵B是矩阵A沿逆时针方向旋转k*90。得到的(要想顺时针旋转,k取-1)
xx = -5:5:40;
yy = polyval(rot90(b,-1));
hold on;
plot(xx,yy,'r')
grid
进行线性回归时,有4个基本假定:
① 因变量与自变量之间存在线性关系;
② 残差是独立的;
③ 残差满足方差奇性;
④ 残差满足正态分布。
在Matlab软件包中有一个做一般多元回归分析的命令regeress,调用格式如下: [b, bint, r, rint, stats] = regress(y,X,alpha) 或者 [b, bint, r, rint, stats] = regress(y,X) 此时,默认alpha = 0.05.
这里,y是一个 的列向量,X是一个 的矩阵,其中第一列是全1向量(这一点对于回归来说很重要,这一个全1列向量对应回归方程的常数项),一般情况下,需要人工造一个全1列向量。
回归方程具有如下形式: 其中, 是残差。 在返回项[b,bint,r,rint,stats]中,
① 是回归方程的系数; ② 是一个 矩阵,它的第 行表示 的(1-alpha)置信区间; ③ 是 的残差列向量; ④ 是 矩阵,它的第 行表示第 个残差 的(1-alpha)置信区间;
注释:残差与残差区间杠杆图,最好在0点线附近比较均匀的分布,而不呈现一定的规律性,如果是这样,就说明回归分析做得比较理想。 ⑤ 一般的, 返回4个值: 值、F_检验值、阈值 ,与显著性概率相关的 值(如果这个 值不存在,则,只输出前3项)。
注释: (1)一般说来, 值越大越好。 (2)人们一般用以下统计量对回归方程做显著性检验:F_检验、t_检验、以及相关系数检验法。Matlab软件包输出F_检验值和阈值 。一般说来,F_检验值越大越好,特别的,应该有F_检验值 。 (3)与显著性概率相关的 值应该满足 。如果 ,则说明回归方程中有多余的自变量,可以将这些多余的自变量从回归方程中剔除(见下面逐步回归的内容)。 这几个技术指标说明拟合程度的好坏。这几个指标都好,就说明回归方程是有意义的。
3.解同余方程组
>> syms n >> solve(mod(n,10) - 9,mod(n,9) - 8,mod(n,8) - 7) Warning: 3 equations in 1 variables. Warning: Explicit solution could not be found. > In solve at 81 ans = [ empty sym ]
注意:matlab里求余不是%也不是mod,而是rem(x,y)
上面的我估计方法不对,懂得指点下!
