问题提出
曲线的拟合和插值,是逼近函数的基本方法,每种方法具有各自的特点和特定的适用范围,实际工作中合理选择方法是重要的。
实验内容
考虑文章《用MATLAB研究多项式插值的振荡现象》中的著名问题。下面MATLAB程序给出了该函数的二次和三次拟合多项式。
x=-1:0.2:1; y=1/(1+25*x.*x); xx=-1:0.02:1; p2=polyfit(x,y,2); yy=polyval(p2,xx); plot(x,y,’o’,xx,yy); xlabel(‘x’); ylabel(‘y’); hold on; p3=polyfit(x,y,3); yy=polyval(p3,xx); plot(x,y,’o’,xx,yy); hold off;
适当修改上述MATLAB程序,也可以拟合其他你有兴趣的函数。
实验要求:
(1)将拟合的结果与拉格朗日插值及样条插值的结果比较。
(2)归纳总结数值实验结果,试定性地说明函数逼近各种方法的适用范围,及实际应用中选择方法应注意的问题。
实验步骤
1.对上述程序适当修改,做出函数y=1/(1+25x2)的(n)次拟合函数并画图,然后分别按相同次的拉格朗日插值做出插值函数并画图,比较两种结果。
2.归纳总结数值实验结果,试定性地说明函数逼近各种方法的适用范围,及实际应用中选择方法应注意的问题。
实验结果及讨论
1. 按上面程序中的多项式插值函数Polyfit,对函数y=1/(1+25x2)做出(n)次拟合,结果为:
如下图所示:次数n=3,6,9,12.
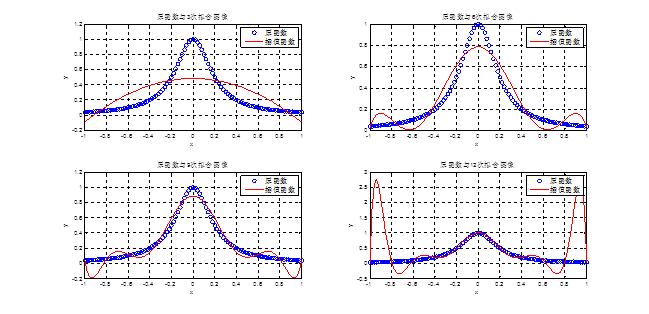
Elapsed time is 0.263684 seconds.
程序源码为:
tic
x=-1:0.02:1;
y=1./(1+25.*(x.*x));
xx=-1:0.2:1;
yy=1./(1+25.*(xx.^2));
p1=polyfit(xx,yy,3); %3次拟合
y1=polyval(p1,x);
p2=polyfit(xx,yy,6); %6次拟合
y2=polyval(p2,x);
p3=polyfit(xx,yy,9); %9次拟合
y3=polyval(p3,x);
p4=polyfit(xx,yy,12); %12次拟合
y4=polyval(p4,x);
subplot(2,2,1);
plot(x,y,'bo');hold on;
plot(x,y1,'r-');hold off;
title('原函数与3次拟合图像');
xlabel('x');ylabel('y');
legend('原函数','插值函数');
grid on
subplot(2,2,2);
plot(x,y,'bo');hold on;
plot(x,y2,'r-');hold off;
title('原函数与6次拟合图像');
xlabel('x');ylabel('y');
legend('原函数','插值函数');
grid on
subplot(2,2,3);
plot(x,y,'bo');hold on;
plot(x,y3,'r-');hold off;
title('原函数与9次拟合图像');
xlabel('x');ylabel('y');
legend('原函数','插值函数');
grid on
subplot(2,2,4);
plot(x,y,'bo');hold on;
plot(x,y4,'r-');hold off;
title('原函数与12次拟合图像');
xlabel('x');ylabel('y');
legend('原函数','插值函数');
grid on
toc
下面是用等距节点的拉格朗日型插值作出的结果:
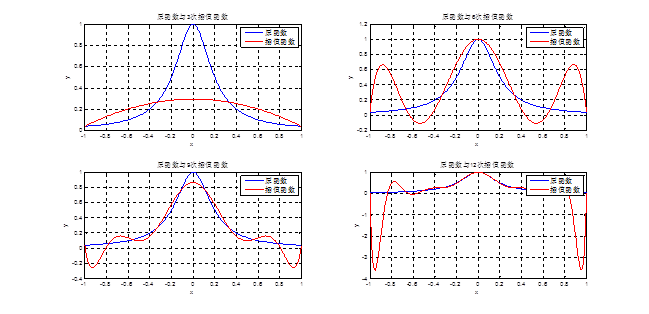
Elapsed time is 2.057597 seconds.
程序源码为:
tic
for n=3:3:12 %n为插值阶数
subplot(2,2,n/3) %将各阶原函数与插值函数的图像分别一张图片上面。
syms x;
f=1/(1+25*x^2); %原函数
x1=sym(zeros(n+1));
W=sym(ones(n+1));
L=sym(0);
for i=0:n
x1(i+1)=-1+2*i/n; %划分等距节点
end
for j=0:n
for i=0:n
if i~=j %求插值基函数
w=(x-x1(i+1))/(x1(j+1)-x1(i+1));
W(j+1)=W(j+1)*w;
end
end
L=L+W(j+1)*(1/(1+25*x1(j+1)^2)); %插值函数
end
LL(n)=simplify(L); %插值函数化简
x=-1:0.01:1;
y1=subs(f,x); %将x带入原函数f中
y2=subs(L,x); %将x带入插值函数L中
plot(x,y1,'b'); hold on;
plot(x,y2,'r'); hold off;
title(['原函数与',num2str(n),'次插值函数']);
xlabel('x'); ylabel('y');
legend('原函数','插值函数');
grid on
end
toc
下面是用切比雪夫节点的拉格朗日型插值作出的结果:
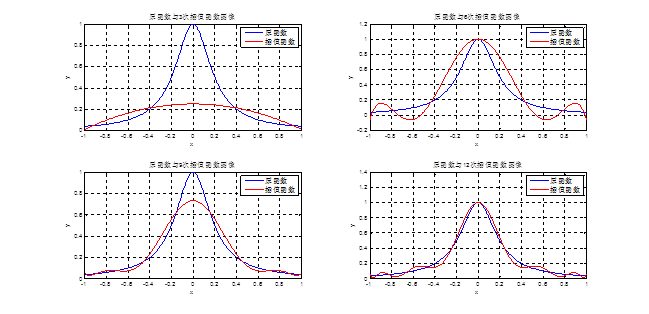
Elapsed time is 2.215264 seconds.
程序源码为:
tic
for n=3:3:12 %n为插值阶数
subplot(2,2,n/3) %将各阶原函数与插值函数的图像分别一张图片上面。
syms x;
f=1/(1+25*x^2); %原函数
x1=sym(zeros(n+1));
W=sym(ones(n+1));
L=sym(0);
for i=0:n
x1(i+1)=cos((2*i+1)*pi/(2*(n+1))); %切比雪夫零点
end
for j=0:n
for i=0:n
if i~=j %求插值基函数
w=(x-x1(i+1))/(x1(j+1)-x1(i+1));
W(j+1)=W(j+1)*w;
end
end
L=L+W(j+1)*(1/(1+25*x1(j+1)^2)); %插值函数
end
LL(n)=simplify(L); %插值函数化简
x=-1:0.01:1;
y1=subs(f,x); %将x带入原函数f中
y2=subs(L,x); %将x带入插值函数L中
plot(x,y1,'b');hold on;
plot(x,y2,'r');hold off;
title(['原函数与',num2str(n),'次插值函数图像']);
xlabel('x');ylabel('y');
legend('原函数','插值函数');
grid on
end
toc
下面是用样条插值作出的结果:
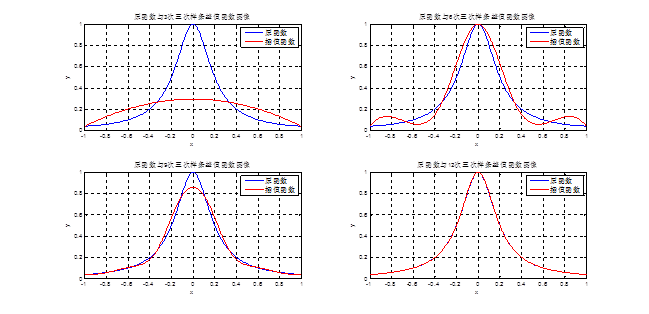
Elapsed time is 0.255934 seconds.
程序源码为:
%本次使用的是三次样条差值。
tic
for n=3:3:12; %插值次数n=3、6、9
x=-1:2/n:1; %等距节点
y=1./(1+25*x.^2); %原函数
x1=-1:0.01:1; %画图取得离散点
y1=spline(x,y,x1); %三次样条差值函数 直接使用spline函数
f=1./(1+25*x1.^2); %原函数,'linewidth',4,'linewidth',2
subplot(2,2,n/3)
plot(x1,f,'b-');hold on;
plot(x1,y1,'r-');hold off;
title(['原函数与',num2str(n),'次三次样条差值函数图像']);
xlabel('x');ylabel('y');
legend('原函数','插值函数');
grid on
end
toc
分析:
从上图可以得出:
1.原函数y=1/(1+25x2)是偶函数,不论使用哪种方法、几次插值所得的的插值函数或拟合函数都是偶函数。所以插值函数或拟合函数的奇偶性跟随原函数,与其一致。
2.拉格朗日插值法的受其节点的控制。当用等距节点插值时,插值函数波动较大,而且出现了龙格现象,算法不稳定。而当用切比雪夫节点插值时,插值函数与原函数之间的误差随着n的增大而减小,没有出现龙格现象,插值函数与原函数越来越逼近。但是拉格朗日插值法当插值节点增减时,计算要全部进行,计算量大,这从上面计算所用时间也可以看出来,拉格朗日插值法所用时间最长。此外,在工程实际应用中,所选节点大多不是切比雪夫节点,所以拉格朗日插值法实际应用中使用较少。
3.多项式拟合函数随着次数n的增高,在区域边界也出现较大的扰动,误差随着n的增大而增大,在高次拟合中也出现了龙格现象。但其误差比等距节点的拉格朗日插值稍低,对于多项式拟合,拟合函数不需要经过每一个节点,且拟合次数与节点数无关,函数的拟合是由节点整体的误差最小所控制,即由minΣ[f(xi)-P(xi)]2控制,而不是各个节点处的函数值控制。这就使得当节点个数增多时,拟合函数在整体误差最小的情况下逐渐与原函数逼近,但有的函数在高次拟合中也会出现龙格现象。
4.从上面样条函数的插值中我们可以看出,三次样条函数与原函数图形之间的误差最小,而且其逼近速度和计算也是最快的,仅用时0.255934s。主要是因为样条插值的节点间距离的最大值随着节点个数的增加而不断减小,而且只使用不超过三次的分段多项式插值,这在增加节点密度的同时避免了高次插值龙格现象的产生,所以样条插值最为精确。
(2)归纳总结数值实验结果,试定性地说明函数逼近各种方法的适用范围,及实际应用中选择方法应注意的问题。
总结:
从以上的分析中我们可以得出:
1.拉格朗日型插值是受插值节点控制的插值方法,它与插值节点选取有密切关系,而且在高次插值时又会产生龙格现象,只有选取切比雪夫零点作为插值节点时才可避免龙格现象。但是在工程实际应用中,所选节点大多不是切比雪夫节点,所以拉格朗日插值法实际应用中使用较少。
2. 样条插值是将插值的区间划分开的低次插值,所以不会发生龙格现象,而且样条插值的光滑性也较高。但是由于它要划分区间,所以它需要有足够多的插值节点。但是,当借点升高时样条插值的计算量比较大。所以,使用时须在耗费时间与光滑性、精度方面做出权衡,
3.多项式拟合中,拟合函数不需要经过每一个节点,且拟合次数与节点数无关,所以一般拟合的次数越高,拟合的效果越好,但是对于有些函数,会出现龙格现象。多项式拟合还需要知道较多的节点,拟合效果才会好。有些函数会在边缘出现龙格现象,如出现龙格现象,应适当降低次数。
总之,在实际工作中,我们要根据实际情况做出选择:
1)如果已知节点很多,且精度要求不高,用多项式拟合较好;
2)如果已知节点不是很多,且精度要求不是很高,用插值比较好;
3)如果精度要求很高,则用样条插值,或者高次的拟合多项式。(注意,若高次拟合中出现龙格现象,则只能用样条插值。)
